consensus law Proof/consensus theorem of boolean algebra [Digital Electronics]

In Digital ELectronics there are various laws and rules for the simplification of boolean functions which are basically used to minimize the complexity of digital hardware design by minimizing the boolean function.

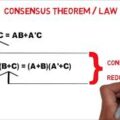
Consensus Law is one of the most powerful theorems used in digital electronics for the minimization of boolean function or equation either in the successive reduction method or in the K-Map method.

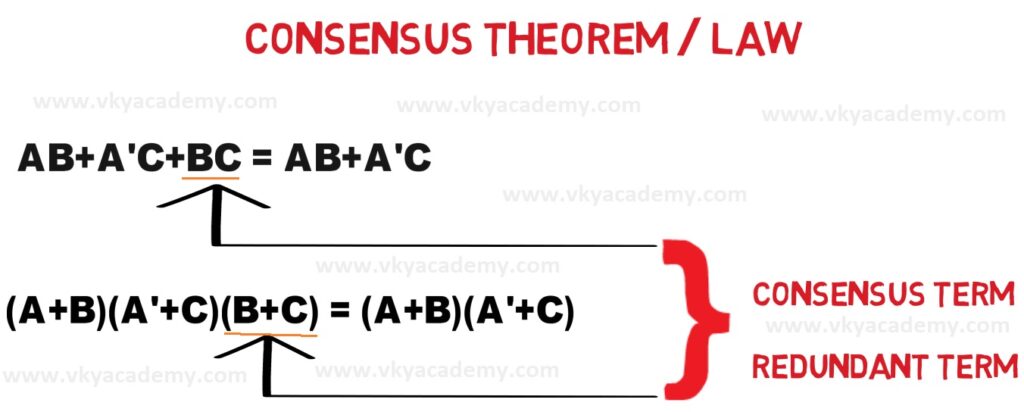
The two important statements of the Consensus Theorem are shown below where we can easily see the term BC in the first statement and the term (B+C) in the second statement doesn’t appear on the Right-hand side or after simplification.

The term BC and the term (B+C) are called consensus term or redundant term as their absence doesn’t make any changes in the final output.

The designer must not use those terms in the equations while designing the complex circuit as their presence may increase the complexity of the digital hardware.

The circuit can be designed on the software tool called DSCH Microwind for the realization and verification of our theorem as shown below.

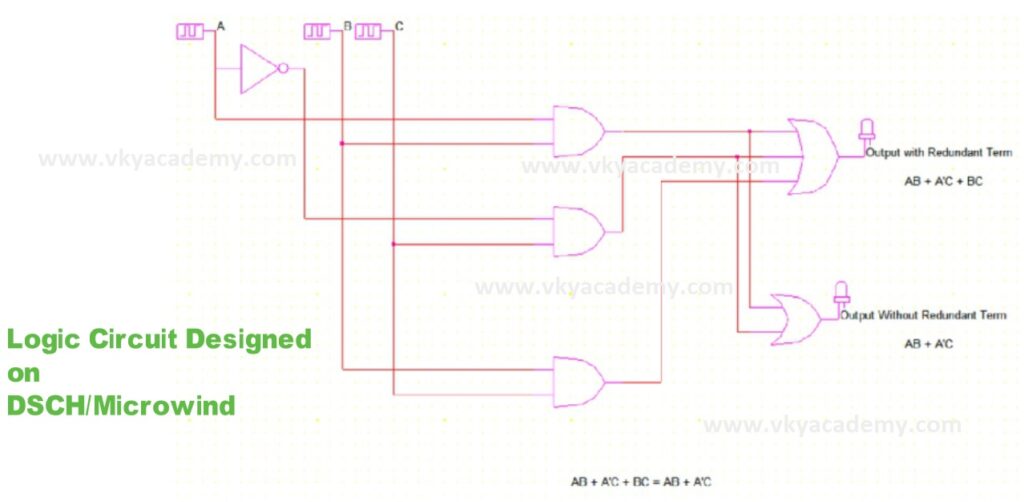
After the design, the circuit is simulated and a “Test Bench Waveform” is generated where we can easily see that the output waveform with the redundant term is the same as the output without redundant term.

Prove of Consensus Theorem/Law :

SOP (Sum of Product ) Statement:

Alternative Method:

POS (Product of Sum) Statement: