Z – Transform and its Applications

Today we will learn, how to determine the Z-Transform and Region of Convergence (ROC) of finite duration Discrete-Time Signal (DTS).

One of the most general and convenient ways of computing the output of an LTI system is by the z-transform.

Z Transform is a powerful mathematical tool that is used for the analysis of LTI DTS.

Z Transform plays the same role in the analysis of discrete time signals and LTI system as the Laplace transform does in continuous time signals and LTI system.

The convolution operation of two discrete-time sequences (DTS) in the time domain is similar to the multiplication of the same discrete-time sequence (DTS) in the Z domain.

As we know multiplication operation is easier than convolution operation.in this way, there are many more things that becomes simpler in the frequency domain as in Z transform.

The Z transform also tells us about the stability of the system.

By using the z-transform, as with many transform techniques, we shift the problem to a different domain (the transform domain), in which the solution, in general, is computed by algebraic operations (straight forward multiplications and divisions).

Like crossing a river, we can either swim straight across to the other side or we can walk to the bridge (the transform domain), cross the bridge (solve the problem in the transform domain).

and walk to the point we want to reach on the other side (go back. to the time domain).

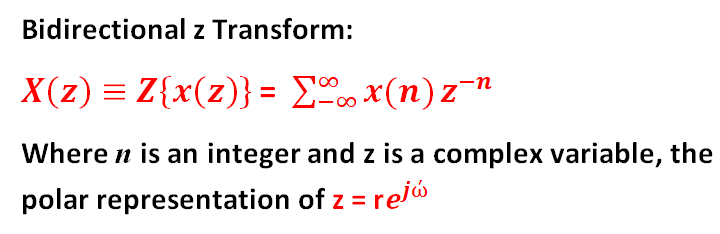
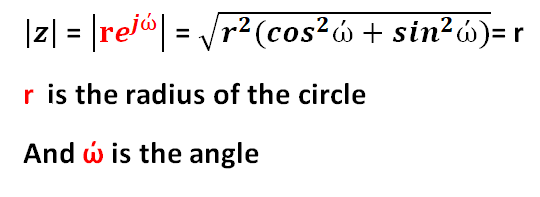
Region of Convergence (ROC):

Since the z transform is an infinite power series, it exists only for those values of z for which the series converges.

Definition:

The ROC of X(Z) is the set of all values of Z for which X(Z) attains a finite value (Converges).

Example-1

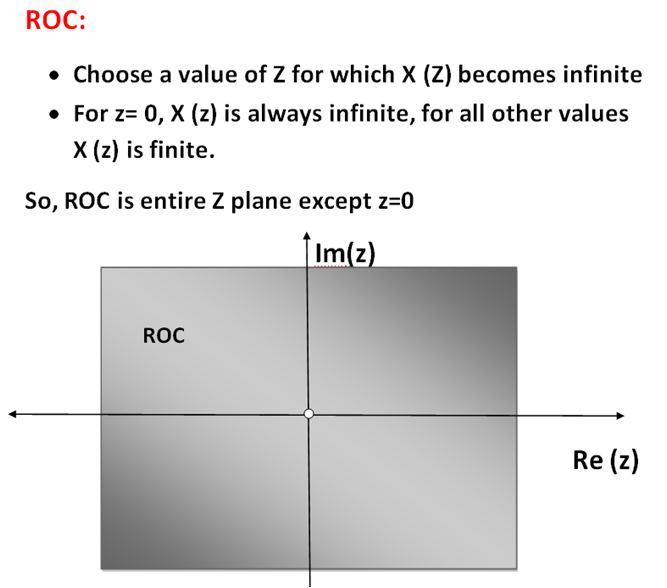
Example-2

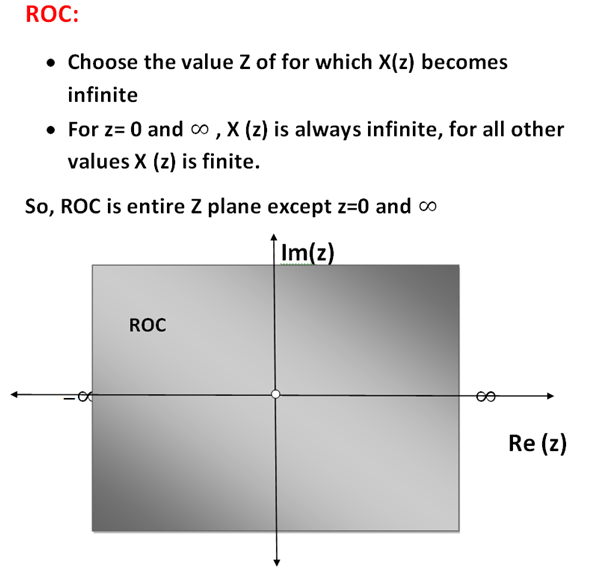
Example-3

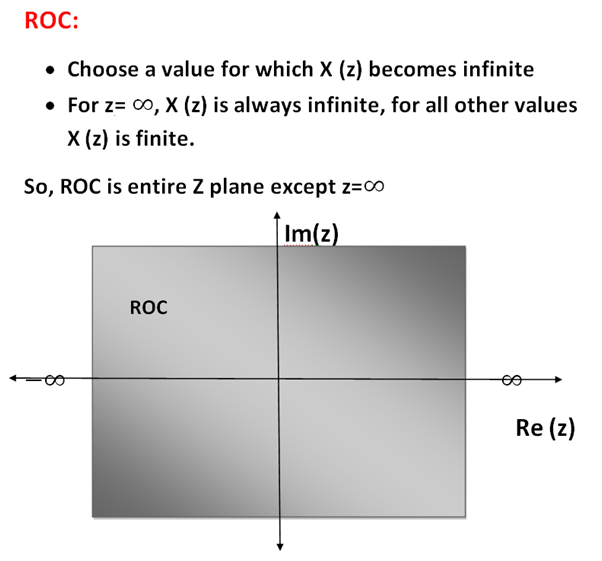
References:

Modern digital signal processing by Roberto Cristi

Digital Signal Processing: Principles, Algorithms, and Applications, 4e
by John G. Proakis and Dimitris G. Manolakis